最近在为数学建模美赛做准备,上次坑了队友,这次不能继续坑下去了,就开始提前准备了=-=
模型简介
Logistic Regression模型,被称为逻辑回归模型或对数回归模型。是一个可以用来解决分类问题的模型,由此模型实现的分类器被称作LR分类器。LR模型可以处理多变量,多类别的分类问题,还是十分全能的。
模型介绍
分类问题是什么
所谓分类问题,就是指给定一个数据集,数据集中的数据分为N个类别,而我们知道所有数据的类别情况。那么我们希望给定一个新的数据,能够根据现有的数据集,判断出新数据是属于哪个类别。
分类问题中比较有名的问题是蝗虫分类问题,比如这里有5个类别,每个类别20只蝗虫的身体数据,其中包括身长,体重,前翅长,后足骨节长等等。那么现在给我们一只新的蝗虫,希望能根据这\(5*20\)个数据立刻给出这个新的蝗虫属于哪个类别。分类问题就是类似这样的问题。
下面就以线性二分类问题,来看看LR模型是怎么工作的。所谓线性二分类,就是指决策边界是线性函数,只有两个类别的分类问题,应该算是最简单的分类问题。
线性回归模型在线性二分类问题上的局限性
遇到分类问题,能不能用线性回归模型来做呢?这显然是不可以的。因为,在分类问题上,比如两个类别的分类问题,我们预期的输出是0和1,代表是属于第一类还是第二类。而线性回归模型是做不到这一点的,因为线性回归模型的输出是有很大的范围的,跟我们期望的输出相差很远。所以,我们就需要做一些操作,把线性回归模型的输出放缩到0到1之间,这样,我们就可以把输出值理解为“可能性”,既直观又靠谱。
LR模型在该问题上的做法
那既然需要对线性回归模型做一些操作,那到底应该做什么操作呢。其实就是一个很简单的操作,比如原来的预测函数为:$h_\theta = \theta^T \cdot x$,其中\(\theta\)是回归系数,是一个向量类型的变量。那么,现在我们只需要做如下操作即可:
\begin{aligned}
h_\theta = g(\theta^T \cdot x) \
g(x) = \frac{1}{1 + e^{-x}}
\end{aligned}
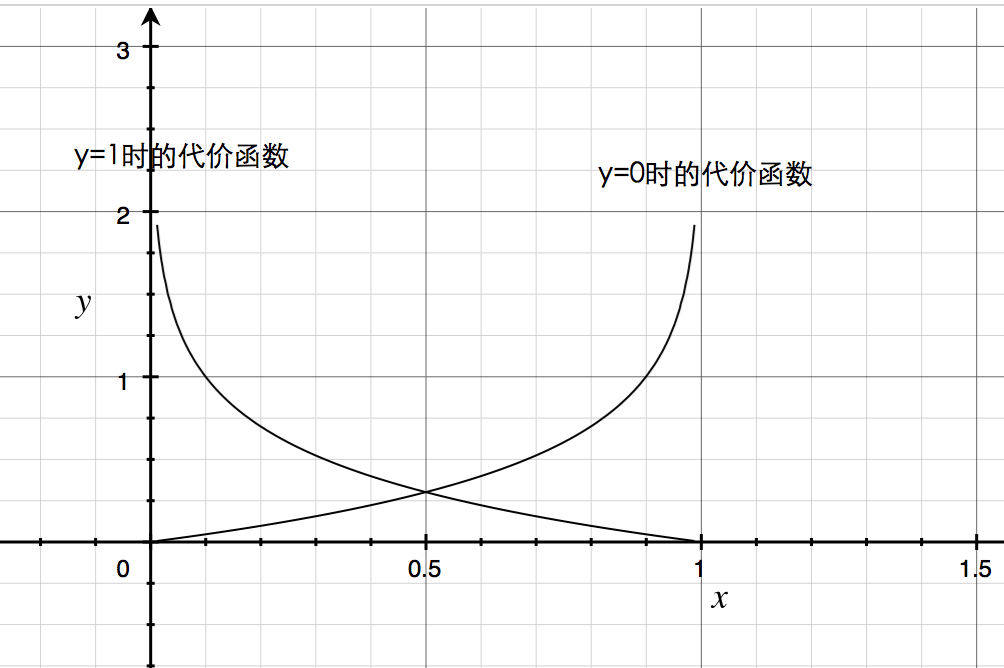
g(x)常常被称作sigmod函数,他连续,光滑,关于(0, 0.5)对称,最主要他的输出在[0, 1]区间上。在这里,$h_\theta$ 的意义是 $P(y=1|x; \theta)$ ,是一个条件概率,意思是在当前的回归系数下,x的输出为1的概率。h函数就是这样,接下来我们需要确定的是回归参数,为此我们需要建立一个代价函数,然后用样本训练。如果是线性二分类,有一个比较好的代价函数:
如果把这个Cost函数的图像画出来,就会发现,当y = 1的时候,如果输出为1,代价为0,越偏向0代价越大,反之亦然。因此,我们需要做的就是求出\(Min_{\theta}(J(\theta))\)。具体做法,就是不断迭代,令\(\theta_j = \theta_j - \alpha \cdot \frac{\partial{J(\theta)}}{\partial {\theta_j}}\),跟线性回归的梯度下降算法实现思路相同,实现难度也不是很大。
LR模型在其他类型分类问题的应用
LR不只是可以处理线性二分类问题,还可以处理更加复杂的问题。主要的变化是\(h_\theta\),其中的X会由一个独立变量组成向量变为变量之间的组合乘积之类的,不过原理是一样的。
有关过度拟合
过度拟合,凭下面一张图估计可以直观的感受到。
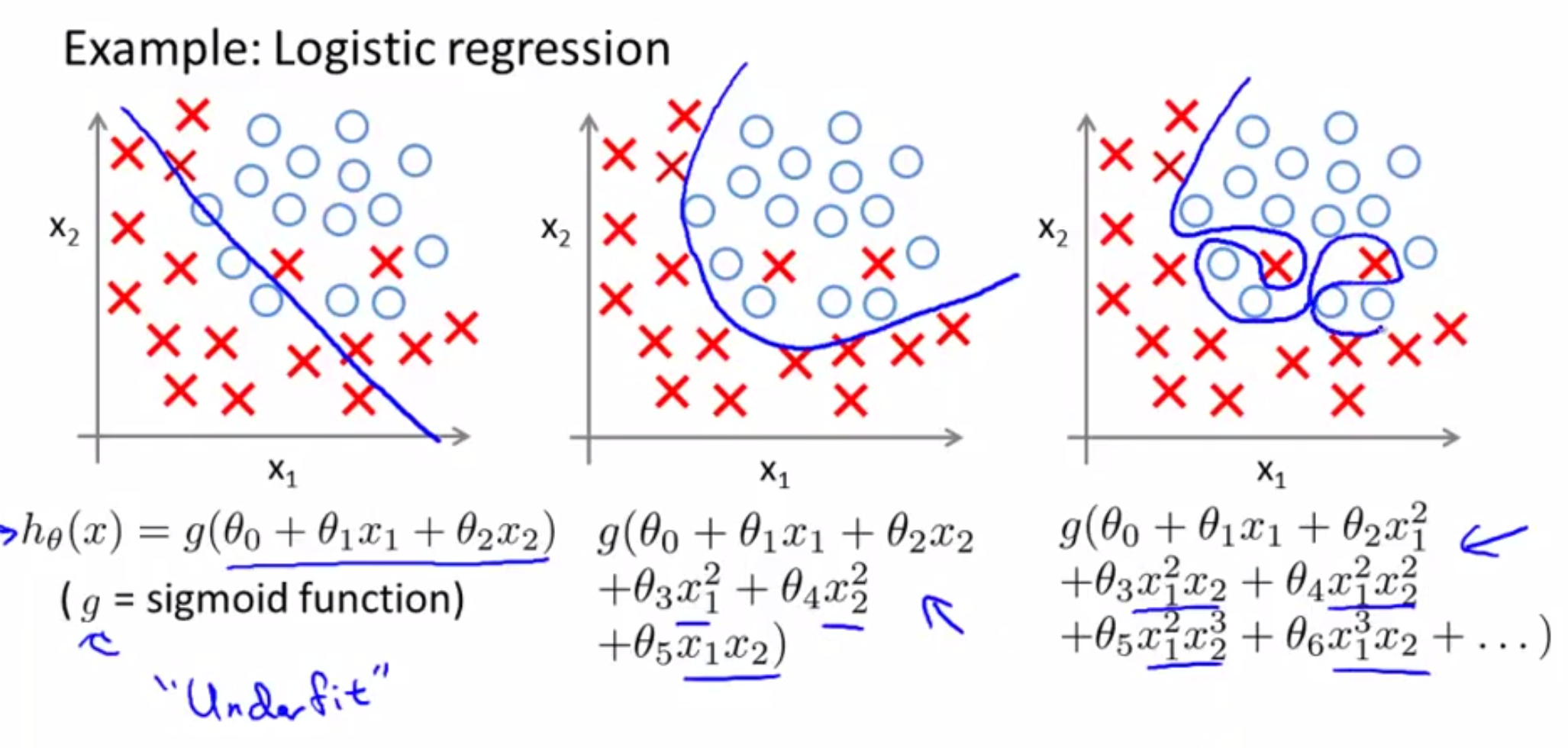
就是指H函数的选择过于复杂,导致决策边界的划定对已有数据非常友好,但是对新数据非常不友好。或者变量的范围不统一,有的变量范围很小,有的变量范围很大,这样就导致了代价函数可能对不同变量的惩罚比重不同,这其实也是很常见的现象。Coursera的Machine Learning课程有专门一个章节在讲如何处理这种情况,其中提出的解决办法主要有两种:
- 降低变量个数
- 正则化变量
对于第一点,可以肉眼判断变量的重要性,这当然是不太科学的。还有的方法就是用算法来进行,比如我能想到的就是主成分分析,得到对这个问题影响最大的变量,这种方式得到的变量是比较科学的。
对于第二点,可以行得通的做法是在代价函数里添加一项:\(\frac{\lambda}{2 \cdot n} \cdot \sum_{i=1}^{m}\theta_j^2\),这样就算变量很多,也会尽可能保证参数是小的,这样在多参数的情况下也能尽量减少过度拟合的情况。
