一致性 (Consistency) 一直是分布式系统里一个很重要的话题, 如果要了解一致性, 要从系统模式开始说起.
系统模型
系统模型 (System Model), 是描述系统的特性的一些假设, 基于这些假设才可以设计出各种各样的分布式系统. 这些假设包括但不限于:
- 每个节点的计算能力以及它们的失效模式
- 节点间通信的能力以及是否可能失效
- 整个系统的属性, 比如时序等等
其中每一点下面都会讲到. 如果一个系统模型是基于最弱的假设的, 比如节点可能出现硬件错误、网络拥塞或断开以及可能遭到恶意攻击等等, 那基于这样的系统模型的分布式系统可以运行在各种各样的环境下, 因为它的容错极高.
而如果我们做出了很强硬的假设, 比如节点不会 fail, 那基于此假设的系统不需要处理节点失效的问题, 但是因为假设太偏离现实, 所以很难在生产环境中真正去使用.
系统模型中的节点问题
节点, 可以理解为系统中的一个个虚拟机或者物理机, 它们是负责真正的计算和存储业务的. 它们会运行确定性的算法, 并且可以将数据写入易失性存储器 (内存) 或者持久性存储器 (磁盘). 不同的存储会受到不同失效模型的影响.
节点的失效模型是指可能使得节点失效的途径. 在大多数实践中, 系统都是假设节点只有在 crash 的时候会失效, 并且会在 crash 之后的某个时间点恢复工作.
这个模型并不是最弱的, 最弱的是著名的拜占庭失效, 也就是可以以任何方式失效. 基于拜占庭失效模型的算法很少在生产环境中遇到, 这也很好想象, 因为实现的难度必然是很大的, 而且大多数时候也遇不到那么多失效的方式. 因此最常用的还是 crash-recovery 模型.
系统模型中的网络问题
在上个年代中, 很少有系统会考虑网络分区的问题, 但是在现在这个环境下, 随着系统的规模增长, 网络的失效也变得常见起来.
一般来说网络的失效模型比较简单, 即直到网络恢复为止, 网络上的信息可能会丢失或者延迟.
系统模型中的时序问题
一般来说, 时序只有两种模式, 异步和同步. 同步是指
Processes execute in lock-step; there is a known upper bound on message transmission delay; each process has an accurate clock
异步是指
No timing assumptions - e.g. processes execute at independent rates; there is no bound on message transmission delay; useful clocks do not exist
也就是说在同步模型中, 信息一定会在一定延迟内送达, 整个系统是有时序的逻辑的. 而在异步模型中, 不存在系统全局的时序.
在现实中, 大部分的场景是部分同步的时序模型, 它们偶尔可以正常工作, 并提供一些上界, 但在某些情况下,消息会被无限期地延迟,时钟也不同步。
共识问题
讨论完系统模型, 接下来就可以在设计好的系统模型的假设下, 讨论共识问题了. 所谓共识 (Consensus) 问题, 就是相互独立的节点之间如何达成一项决议的问题。通俗来说, 如果多个相互独立的节点都认同同一个结果, 那他们就达成了共识. 形式化的描述就是:
- 认同 (agreement): 一个决议过程中所有 N 个节点都认同一个结果
- 合法 (validity): 该结果必须由 N 个节点中的节点提出
- 可结束 (termination): 决议过程在一定时间内结束,不会无休止地进行下去
这个听上去很简单, 但是在比较弱的系统模型下, 有很多问题会导致共识是很难达成的. 比如如果网络中存在消息延时、丢失,节点间消息传递; 亦或者是节点存在 crash 的情况. 在这些假设下, 如何达成共识, 才是真正对现实中的分布式系统有价值的讨论.
FLP 定理
这里就不得不提到一个定理: FLP 定理. 该定理的论文是由 Fischer, Lynch and Patterson 三位作者于1985年发表,之后该论文获得了 Dijkstra 奖。定理所依赖的系统模型很简单:
- 节点只会因为 crash 而失效 (非拜占庭失效)
- 网络是可靠的, 只要进程非失败,消息虽会被无限延迟,但最终会被送达;并且消息仅会被送达一次 (无重复)
- 异步的时序模型, 与同步通信的最大区别是没有时钟、不能时间同步、不能使用超时、不能探测失败、消息可任意延迟、消息可乱序
在现实中,一般网络会使用 TCP 协议 (保证了消息健壮、不重复、不乱序),每个节点都有 NTP 时钟同步 (可以使用超时), 如 FLP 定理的系统模型这样的异步场景相对比较少. 但是也还是存在一定的场景.
FLP 在这样的系统模型下给出了一个很吃鸡的结论: 在异步通信场景,即使只有一个进程失败,也没有任何 (确定性) 算法能保证非失败进程达到一致性.
也就是说, 解决共识问题的算法必须在不存在消息传递边界的情况下放弃强一致 (safety) 或者可用性 (liveness)。
CAP 理论
CAP 恐怕要比 FLP 定理更出名一些. 甚至国内某 NewSQL 数据库厂商 PingCAP 把它加入了自己公司的名字中.
这一理论是说
- 强一致性 (Strong Consistency): 如果系统对一个写操作返回成功,那么之后的读请求都必须读到这个新数据;如果返回失败,那么所有读操作都不能读到这个数据,对调用者而言数据具有强一致性
- 可用性 (Availability): 节点的失效不会导致其余节点的工作收到影响
- 分区容错性 (Partition tolerance): 在网络分区的情况下,被分隔的节点仍能正常对外服务
C、A、P 三者最多只能满足其中两个,和 FLP 定理一样,CAP 定理也指出了一个不可达的结果 (impossibility result)。
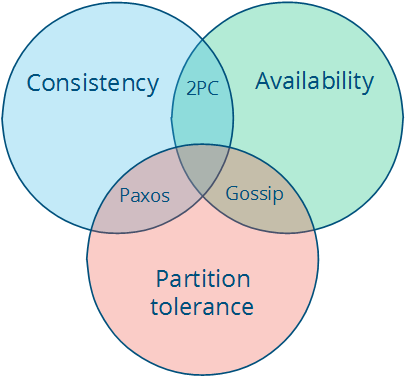
但是需要注意的是, 这里的 C 指的是强一致性, 而非一致性. 因此在现实中, 一致性的强弱与可用性是可以 trade-off 的. 那因此就存在一致性的模型.
一致性模型
一致性模型是描述一致性强弱的. 大类可分为强一致性和弱一致性模型. 但是其中又有很多小的不同.
其中强一致性模型主要是有两种, 一种是线性一致性 (Linearizable consistency), 另一种是顺序一致性 (Sequential consistency).
关键的区别在于,线性化的一致性要求操作生效的顺序等于实际的实时操作排序。顺序一致性允许操作被重新排序,只要在每个节点上观察到的顺序保持一致。作为用户, 能区分两者的唯一方法是,观察系统的所有输入和时间. 从客户端与节点交互的角度来看,两者是等价的。
而弱一致性则是有以客户为中心的一致性模型 (Client-centric consistency models), 因果一致性 (Causal consistency) 和最终一致性 (Eventual consistency).
其中客户为中心的一致性模型可能保证客户永远不会看到数据项的旧版本。这通常是通过在客户端库中构建额外的缓存来实现的,因此,如果客户端移动到包含旧数据的副本节点,那么客户端库就会返回缓存的值,而不是从副本中返回旧值。
最终一致性是系统保证如果没有对某个对象的新更新操作,最终所有的访问将返回这个对象的最后更新的值。这里就有比较多的取舍了, 比如最终是多久之类的.
因果一致性可以理解为是最终一致性的变种, 如果进程 A 通知进程 B 它已经更新了一个数据项,那么进程 B 的后续访问将返回更新后的值,并且写操作将被保证取代前一次写入。和进程 A 没有因果关系的 C 的访问将遵循正常的最终一致性规则。
参考文章
License
- This article is licensed under CC BY-NC-SA 3.0.
- Please contact me for commercial use.
