问题描述
KMP算法,是用来解决字符串匹配问题的。字符串匹配问题,就是给定一个pattern串,一个text串,找出pattern串是否出现在text中,出现在什么位置等等。KMP算法可以在O(len(text))的时间复杂度做完。
思想与实现
要介绍KMP算法,首先要介绍的最简单的字符串匹配的做法。最简单的做法就是依次对于text中的子串与pattern串进行比对,这样做的时间复杂度为O(len(text) * len(pattern)),思想很简单。KMP算法跟最朴素的算法之间的区别在于,KMP算法只需要扫描一遍text串,不会出现朴素算法中回溯的情况。
有限自动机的理解方式
最容易理解的实现是借用了有限状态机的思想,pattern串构成了一个有限状态自动机,共有len(pattern) + 1个状态。状态的转移是KMP算法可以达到O(len(text))的时间复杂度的关键。
public KMP(char[] pattern, int R) {
this.R = R;
this.pattern = new char[pattern.length];
for (int j = 0; j < pattern.length; j++)
this.pattern[j] = pattern[j];
// build DFA from pattern
int M = pattern.length;
dfa = new int[R][M];
dfa[pattern[0]][0] = 1;
for (int X = 0, j = 1; j < M; j++) {
for (int c = 0; c < R; c++)
dfa[c][j] = dfa[c][X]; // Copy mismatch cases.
dfa[pattern[j]][j] = j+1; // Set match case.
X = dfa[pattern[j]][X]; // Update restart state.
}
}
public int search(String txt) {
// simulate operation of DFA on text
int M = pat.length();
int N = txt.length();
int i, j;
for (i = 0, j = 0; i < N && j < M; i++) {
j = dfa[txt.charAt(i)][j];
}
if (j == M) return i - M; // found
return N; // not found
}
在碰到不能全部匹配pattern串的时候,状态机不是简单地回到开始状态重新匹配,而是进行向之前状态的转移,这些转移可以保证text的读入不需要回溯,所以可以看到在search函数中只有一个len(text)次的循环就可以完成判断。
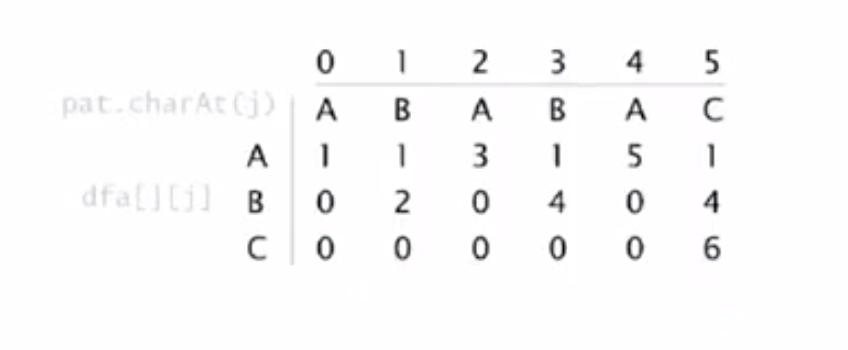
前缀后缀的理解方式
这种方式我觉得理解起来比有限状态机困难一点,不过本质是一样的,都是源自pattern串的跳跃。这种方法需要维护一个数组,数组存储pattern串的前缀等于后缀的的长度。这个数组的size就是pattern的size,可以将它命名为next数组,因为它的作用在于使得pattern匹配不成功时跳到合适的位置。举例说明~
index 0 1 2 3 4 Pattern A B A B C next 0 0 1 2 0
如果text串匹配到了”ABAB”,但是后面不是”C”,那么有了next函数,我们的pattern会继续尝试匹配2,也就是看是不是”A”,这样可以有效防止回溯。我觉得这种方式挺难理解的,反正我是想了好久才有点理解。
